Home  ›  The Wages of Failure: New Evidence on School Retention and Long-run Outcomes

The Wages of Failure: New Evidence on School Retention and Long-run Outcomes

Written By Tuesday 14 December 2021 Add Comment Edit

Abstract

Grade retention has been the focus of the education debate in Spain for decades. On average, more than 30% of students have repeated at least one grade before they finish (or dropout from) their compulsory studies. The present research provides new evidence on this issue by investigating the influence of Spain's school entry age upon students' grade retention. Using data from 15-year-old students who participated in the PISA 2006, 2009, 2012 and 2015 assessments, we implement a regression discontinuity analysis. Our key finding is that students who were born late in the year (younger students) are more likely to repeat a grade. Yet, once they reach secondary education, the disadvantage they suffer due to their younger school starting age seems to disappear. Hence, the key reason why younger students have lower PISA scores than older students in Spain is due to their increased likelihood of repeating a grade, rather than being due to their relative age per se. To avoid these artificial disadvantages of younger students and unfair retention, we suggest that policymakers inform families about this school entry issue and also make the school entry law more flexible. This would facilitate parents of younger children to choose whether to delay their children's school enrolment or not.

Introduction

This paper investigates how school entry regulations may influence students' academic outcomes and, particularly, students' likelihood of grade retention, focusing upon the case of Spain. First, regarding school entry regulations, it is common for education systems to set an entry cut-off (or threshold age) for children to start compulsory education. This legislation varies depending on the country. In France, for example, students typically start their compulsory studies the year they turn 6 years old. Yet French parents also have the discretion to advance or delay their child's enrolment in school depending upon their level of maturity. Similarly, in Croatia, students typically start school in the September of the year that they turn 7, but this school entry can be advanced by parents so that their child can start at age 6. Footnote 1 In Finland, children usually start school during the calendar year of their 7th birthday, but parents have the option to enrol their child 1 year earlier or later. Footnote 2 Although these arbitrary cross-national differences in school entry cut-off regulations may seem unimportant at first, it is not a trivial issue. Indeed, previous research has suggested that students who start school younger than their classmates also tend to be less mature than their older classmates, which may result in lower academic performance and higher likelihood of grade retention (e.g. Bedard & Dhuey, 2006).

The latter (grade retention) is the focus of this research. The education laws of each country not only differ in terms of students' school starting ages, but also in the way they manage the progression of students from one academic year to the next. For instance, in countries like Iceland, grade retention does not exist, so students are automatically promoted to the next grade. Similarly, in the UK, grade repetition—or placement into "out of year-group"—only occurs in exceptional circumstances. On the other hand, in many other countries, students may repeat a grade depending upon the subjects they have failed—e.g. Austria, Greece, Ireland, Portugal, France, Spain—(Eurydice, 2011). Authors such as Goos et al. (2013) note how the likelihood of grade retention is heavily influenced by country level factors. This includes national education policy, historical traditions and societal beliefs about the pros and cons of students repeating a grade. These national differences are reflected within the wide variation in grade retention rates across countries in the OECD's Programme for International Student Assessment (PISA). For instance, in 2015, the retention rate in Austria was 7%, compared to 5% in Greece, 7% in Ireland, 31% in Portugal, 22% in France and 31% in Spain (OECD, 2016). Note that Spain—the setting for this research—has one of the highest levels of grade retention across the OECD (the OECD average is 13%). This becomes even more alarming when knowing that 20% of Spanish students dropped out their studies in 2015 without finishing compulsory education (IECA, 2021).

This grade retention issue is relevant as it extends to other aspects of society such as, for instance, the high monetary and social costs from students repeating and dropping out their compulsory studies, which are rooted in low academic achievement or selection of inappropriate academic track (Angrist & Krueger, 1991). Regarding monetary costs, CCOO Footnote 3 (2018) indicated that re-enrolling all those students who dropped out of compulsory education (so that they can finish it) in Spain in 2015 would cost around 3.2 billion Euros. There is also a high cost for society, as a positive correlation has been found between education, productivity and economic growth (Asteriou & Agiomirgianakis, 2001; Cabus & De Witte, 2012). The importance of this dropout problem has been indicated in the Lisbon Agenda and in the "Horizon 2020" programme of the European Union, which defined policy interventions oriented to reduce the early school dropout rate to 10% by 2020.

Within the present study, grade retention has been analysed considering the theoretical framework of social stratification theory (DiPrete & Eirich, 2006), in which triggering events and scarring are important cornerstones. In particular, within this theoretical framework, scarring indicates a seminal life-course event that has a long-lasting effect that impacts upon subsequent outcomes, typically in a negative way. This theory has been applied to many fields, including the context of educational progression by authors such as, e.g., Andrew (2014). This explicitly considered grade retention to be a scarring event, which requires its particular analysis to correctly assess its consequences. Thus, it is this "scarring" effect of grade retention that we consider in this study.

Combining these two issues (school entry age and grade retention), the lack of maturity of younger students is likely to mean that they are at greater risk of being forced to repeat a school grade (Eide & Showalter, 2001). This paper presents new empirical evidence on this matter, illustrating how the likelihood of grade retention varies by month of birth in Spain, where students must start compulsory education school (1st grade) in the same calendar year of their 6th birthday. Footnote 4 This means that the school entry cut-off is set between the 1st January and the 31st December of students' 6th birthday year. Unlike other countries, in Spain, parents do not have any room to delay or advance their children's school entry date. Consequently, those students born late in the year (e.g. December) are younger than those born sooner (e.g. January), although both have to attend the same grade. The former students may hence also be less developed than older students (both mentally and physically) when they start school (Agasisti & Cordero-Ferrera, 2013; Alet, 2010; Pedraja-Chaparro et al., 2015). This, together with the fact that primary school students in Spain can repeat a maximum of one primary and two secondary school grades, potentially creates a perfect storm for children who have the misfortunate to be born at the end of the calendar year.

Specifically, the research question that we attempt to answer is:

Is the school entry cut-off set in the Spanish education law artificially creating repeater students?

Our work is novel in at least two ways. First, this is the first time that this issue has been explored for the whole of Spain using a methodology (i.e. regression discontinuity) which gets closer to a causal effect than standard regression analyses. Second, by pulling data together from across four PISA cycles (2006, 2009, 2012 and 2015), during which school entry cut-off and grade retention laws remained the same, we maximise both the sample size and the statistical power of our results.

The rest of the paper is structured as follows: first, we provide a literature review of grade retention and school entry cut-off research studies; then, a description of the data and methodology used is presented, followed by the results of this analysis, discussion and conclusions.

Literature review

The study of grade retention

Most of the literature has found grade retention to be negatively associated with students' academic performance, which may result in school dropout. Glick and Sahn (2010) studied grade retention for primary school students in Senegal, finding they were more likely to drop out after being held back. Similarly, Ou and Reynolds (2010) analysed the relationship between grade retention and participation in postsecondary education in Chicago. They found that those who repeated a grade later were more likely to not complete postsecondary education. Other authors such as Andrew (2014) studied grade retention for primary education students in the USA, finding a negative association with high school completion. On the other hand, Jacob and Lefgren (2009) indicated that grade retention did not influence the likelihood of high school completion for students in 6th grade in Chicago, but grade retention in 8th grade did. This was due to sixth graders having more time to catch up after being retained.

Another strand of the literature highlights how grade retention does not influence students' academic performance. For instance, Eide and Showalter (2001) used an instrumental variable approach in the USA (exploiting exogenous variation across states in kindergarten entry dates) and found no significant associations between grade retention and either (a) dropping out of school or (b) labour market earnings. Others such as Jimerson (2001) performed a meta-analysis on 20 studies, finding that grade retention did not lead to better results than automatic promotion, suggesting that alternative remedial strategies should be used. Similar results have been found by Jimerson and Kaufman (2003) and Jimerson et al. (2005). A null association between grade retention and students' academic performance was also found by Allen et al. (2009), based upon a meta-analysis of 22 studies.

Regarding Spain, although grade retention has been increasingly studied, most of the evidence is based on correlational research. This is likely due to the lack of experimental and longitudinal education data in this country. For instance, Carabaña (2013) explored PISA 2012 data for Spanish secondary education students, finding that grade retention in primary education was the best predictor of grade retention in secondary education. He also found that grade retention was associated with both cognitive factors (e.g. academic performance) and non-cognitive factors (e.g. students speaking different languages in the classroom). Gortazar (2019) presented a report of the Spanish education system (with PISA 2015 data) using descriptive statistics and correlational analyses. This author found a relationship between grade retention and school dropout, thus indicating that grade retention negatively influences future career development as a result. Similarly, Calero et al. (2010) used PISA 2006 data to show a positive association between grade retention and school dropout in Spain.

There are some other studies which have tried to overcome the lack of experimental and longitudinal education data in Spain using different resources and methodological techniques. García-Pérez et al. (2014) analysed grade retention for secondary education students using PISA 2009 data and a switching regression model, using students' quarter of birth as an instrumental variable. They found that grade retention had a negative influence on students' academic performance, with there being a stronger influence upon students who repeated grades in both primary and secondary school. Other authors such as Choi et al. (2016) used a combination of cross-sectional data from the Progress in International Reading Literacy Study 2006 (PIRLS) and PISA 2012 to create a pseudo-panel. They found a negative association between grade retention and academic performance in Spain.

However, there is not any evidence—to the best of our knowledge—on the likelihood of grade retention in Spain that attempts to move beyond correlation to causation. We attempt to address this issue here by using a regression discontinuity design, based upon the sharp discontinuity created by Spain's school entry laws. This, we argue, allows us to get closer to causality than much of the existing literature. In the following, we describe the literature on this methodology and the use of school entry age as a cut-off.

The use of school entry cut-off

Much previous work has investigated the influence of school entry age on students' academic performance, with most studies using month or quarter of birth to explore this issue. Most find that younger students (relative to their classmates) have lower levels of academic performance. For instance, Bedard and Dhuey (2006) analysed 4th grade students who participated in the Trends in International Mathematics and Science Study (TIMSS) in 19 OECD countries (including Spain); they found that younger students achieved lower scores on average than older students. Similar results were found by Alet (2010) for 1st grade students in France Footnote 5 and by Agasisti and Cordero-Ferrera (2013) for 15-year-old Spanish and Italian Footnote 6 students for PISA 2006 data. Sprietsma (2010) considered the influence of school entry age using a regression discontinuity approach and the national rules for admission to primary education for 16 countries using data from PISA 2003. They found a positive influence of age on test scores in half of the countries and regions considered. Interestingly, they also found that the relative age effect in Spain was mainly driven by grade retention, concluding that there is no "residual" performance difference between older and younger students once controlled by grade retention. Other authors, such as Wallingford and Prout (2000), showed that 5th grade American students who were born in summer (i.e. younger students, as the school entry cut-off was set just before that season) were more likely to attend special education. Nevertheless, Anders et al. (2016) analysed PISA 2009 data for 15-year-old students in Shanghai and Chinese Taipei, making use of their school entry policy (which made similarly aged students to be found in different grades, depending on if they were born in August or September). Students in these countries were found to make little progress over one whole secondary school year. Others like Crawford et al. (2014) explored this issue for 7-year-old students in England, finding that cognitive scores were only influenced by their age when they took the test, and not by differences in relative age at school entry.

Regarding the use of school entry age to analyse grade retention, evidence is quite scarce. One important exception is Manacorda (2012), who used a discontinuity in the grade failure legislation in Uruguay (students automatically repeated with three failed subjects). They found that this legislation increased the dropout rate while also lowering levels of academic achievement. For Spain and France, Pedraja-Chaparro et al. (2015) found that students born in the final months of the year were 70 to 80% more likely to repeat a grade (based upon PISA 2009 data). These results may, however, be the consequence of using a simple regression analysis, as we will illustrate in Sect. 6. Many research studies have also combined grade retention with regression discontinuity approach, drawing upon test score cut-offs for grade retention (i.e. the test score which has to be surpassed by students in order to pass) to analyse diverse outcomes such as students' behaviour (Özek, 2015; Martorell & Mariano, 2018; Diaz et al., 2016, dropout (Eren et al., 2017; Mariano et al., 2018 and academic achievement (Schwerdt et al., 2017). However, relatively few studies have used school entry cut-offs to analyse grade retention, as we do in this study. Important exceptions include Bernardi (2014), who investigated the link between school entry cut-offs and grade retention in France, and Cook and Kang (2016), who used a regression discontinuity design to explore how school entry cut-offs impacted grade retention of students aged 11 and 15 in North Carolina. Both of these studies found being young relative to school peers to be related to greater chances of repeating a grade.

Similar to our research, Dicks and Lancee (2018) analysed the influence of the school entry cut-off on French students' likelihood of grade retention using PISA 2009, 2012 and 2015 data. They found younger students were 9% more likely to repeat a grade during primary school. The present paper adds to this literature by being the first to investigate the influence of school entry cut-off on the likelihood of grade retention in Spain using a regression discontinuity approach, drawing upon data with a particularly large sample size (i.e. PISA 2006, 2009, 2012 and 2015 waves).

It is important to note that previous work using month or quarter of birth to investigate students' outcomes (as, e.g., academic achievement or grade retention) has received some criticism. For instance, Barua and Lang (2016) criticised the use of the quarter of birth as an instrumental variable in the context of the USA, suggesting that it does not satisfy the monotonicity property. Footnote 7 Specifically, they argued that some parents may delay the enrolment of their children in school to avoid them being younger than their peers, whereas other parents may enrol their children independently of their relative age. The influence of the quarter of birth will then not be the same for both groups. Similarly, Buckles and Hungerman (2013) argued that quarter of birth is not a proper instrument, as it may be influenced by the different fertility patterns of different socio-economic groups. However, as we will detail in Sect. 4, such arguments do not seem to hold in the context of Spain. In particular, we show how younger students have consistently higher rates of grade retention in Spain, births are randomly distributed across the year and—critically—parents are unable to delay or advance the enrolment of their children in school.

Data

Our data are drawn from the Programme for International Student Assessment (PISA). PISA started in 2000 and has been conducted every 3 years since. PISA's objective is to assess 15-year-old students' skills in reading, mathematics and science. In Spain, participants are in the fourth and final year of secondary education Footnote 8 (i.e. tenth grade, unless they have repeated a grade). PISA employs a stratified, clustered sample design, with schools being the primary sampling unit. Further contextual information about students and schools is also gathered. We use data from all PISA cycles in which a representative sample was drawn for most of Spain's regions (2006, 2009, 2012 and 2015 Footnote 9). This leads to a total sample of 102,534 students (72,223 non-repeaters, 22,893 repeaters of one grade and 7418 repeaters of two grades).

Within the background questionnaire, students reported their day, month and year of birth. Unfortunately, exact day of birth is not publicly released by the OECD. Hence, we use month of birth within our identification strategy.

The use of PISA data requires employing the OECD's recommended analysis procedures. This involves applying the final student weights and balanced repeated replication (BRR) Footnote 10 weights throughout the analysis, as well as using the so-called plausible values (see OECD, 2009, for further details). We follow these recommended practices throughout this paper (see Jerrim et al., 2017, for further details). Students' scores have also been standardised—using the Spanish mean and standard deviation—for each PISA cycle (OECD, 2007, 2010, 2014, 2016). All estimates are therefore reported in terms of effect sizes.

Methodology

Within this section, we describe our regression discontinuity procedure and whether the assumptions underpinning this approach are met.

Checking for exogenous variation

First, the school entry cut-off has to be a source of exogenous variation. The school entry cut-off dates have been set by Spanish law and have not changed over the time period we consider (students start school near middle September the year of their sixth birthday; BOE, Footnote 112002, art. 9.1; 2006, art. 16.1; 2013, art. 4.1). Moreover, parents are unable to delay or advance school enrolment. Together, this means it seems reasonable to assume that school entry cut-off dates are a source of exogenous variation. Similarly, grade retention laws also did not change over this period (students can repeat once in primary education Footnote 12 and twice in secondary education Footnote 13) and are determined by an objective criterion: students who fail at least three subjects Footnote 14 must repeat the grade. This means pooling data from across four PISA cycles (2006, 2009, 2012 and 2015)—during which school entry cut-off and grade retention laws were kept the same—will maximise the precision of our results.

Checking for discontinuity in covariates

Our regression discontinuity approach assumes that students' month of birth should be as good as randomly assigned (at least at the discontinuity). In our application, this means that children born in January (the oldest) and December (the youngest) should be the same in terms of both observable and unobservable characteristics (in expectations). We can check if this is the case for observable characteristics using a test of mean differences. This comparison is presented in Table 6 (Appendix). There is little difference between students born in January and December in terms of key background characteristics (sex, maternal and paternal education and number of books at home). Table 7 (Appendix) generalises this finding to show that this holds for comparisons across all birth months. This suggests that Spanish parents do not seem to manipulate their child's month of birth, at least by these key socio-economic characteristics.

Another key characteristic of PISA data is that it includes only 15-year-old students (independent of the grade they are attending). Students are therefore not lost due to positive selection, as happens when full classes from a particular grade are sampled (such as in PIRLS and TIMSS). Footnote 15

Checking for continuity of the density

Figure 1 illustrates how 15-year-old student births in Spain are randomly distributed across the academic year. In other words, there is little evidence of seasonality of birth dates, which is important for our regression discontinuity approach. Interestingly, Fig. 1 also illustrates how grade repeaters are more likely to be born later in the calendar year. This takes us to our final test.

Fig. 1
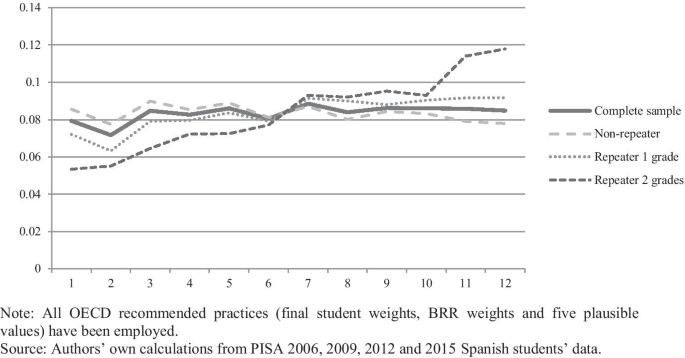
figure1

Distribution of births in the year by grade retention. Note: All OECD recommended practices (final student weights, BRR weights and five plausible values) have been employed. Source: Authors' own calculations from PISA 2006, 2009, 2012 and 2015 Spanish students' data

Full size image

Checking for discontinuity in the outcome variables

Finally, the exogenous variation (i.e. birth month) should influence our variable of interest (i.e. grade retention). As Table 6 (Appendix) illustrates, students born later in the year are indeed more likely to repeat a grade. Students' birth month hence seems to fulfil the monotonicity property, as:

  • The likelihood of grade retention seems to increase as one moves from January to December.

  • Students' month of birth is random (as illustrated by the similar characteristics of students born in each month).

  • Parents cannot delay or advance the school enrolment of their child.

Regression discontinuity model

Having satisfied the assumptions underpinning regression discontinuity designs, we now present the statistical model we use to implement this approach. First, we begin by restricting the sample to students born just before (December) and just after (January) the cut-off. We then estimate the following model using Ordinary Least Squares (OLS):

$${GR}_{ij}=\alpha +\beta {CO}_{ij}+\gamma {X}_{ij}+{\varepsilon }_{ij}$$

(1)

where \(i\) represents the student and \(j\) the school; \({GR}_{ij}\) measures grade retention and takes the value "1" when the student has repeated (1 or 2 grades or both, depending on the specification) and "0" when the student has not repeated; \({CO}_{ij}\) is the school entry cut-off variable, which takes the value "1" when the student was born just before the cut-off (i.e. December) and "0" when the student was born just after the cut-off (i.e. January); \({X}_{ij}\) are student observable characteristics; \({\varepsilon }_{ij}\) is the idiosyncratic error term.

Students' observable characteristics (\({X}_{ij}\)) include sex and socio-economic status. Footnote 16 These variables have previously been found to explain grade retention, with girls less likely to repeat than boys (Tingle et al., 2012) and lower socio-economic status students more likely to repeat than their high socio-economic peers (Mattison et al., 2018). Other studies have analysed both gender and socio-economic status simultaneously, finding similar results (García-Pérez et al., 2014; González-Betancor & López-Puig, 2016; Klapproth & Schaltz, 2015; Pedraja-Chaparro et al., 2015).

We have to highlight that, as we only have the month of birth and not the exact date of birth, we cannot obtain a causal effect of the cut-off; furthermore, there may be some other unobservables which we are not able to control for. Because of these reasons, we are cautious and interpret our results as conditional associations. Additional robustness checks complement our main estimations.

Results

The main results are presented in Table 1. Younger students (December born) are 4.3% more likely to repeat once and 4.8% more likely to repeat twice than older students (January born). If we focus on the total likelihood of grade retention, younger students are 11.1% more likely to repeat than older students. Footnote 17

Table 1 Relationship between students' month of birth and likelihood of grade retention

Full size table

At first sight, it may also seem that younger students have lower levels of academic achievement than older students as well. This is illustrated by Figs. 2a, 3a and 4a, for each PISA subject, respectively. Yet this may not actually be the case, at least once students reach secondary education. Footnote 18 This is illustrated by Figs. 2b, 3b and 4b, which present average PISA scores by month of birth, stratified by grade retention. In particular, note that average standardised scores are now similar across birth months. We move from this descriptive analysis to our regression discontinuity approach to confirm this result. The benefit is that the latter controls for many variables that the descriptive analysis does not. In order to do this, we replicate the main estimations presented in Table 1 using, alternatively, students' reading, mathematics and science standardised scores as the dependent variable. These estimations can be found in Table 2. This illustrates how younger students perform almost 0.15 standard deviations lower than the older students, when using the full sample. However, when dividing the sample by grade retention, the association between birth month and PISA scores disappears.

Fig. 2
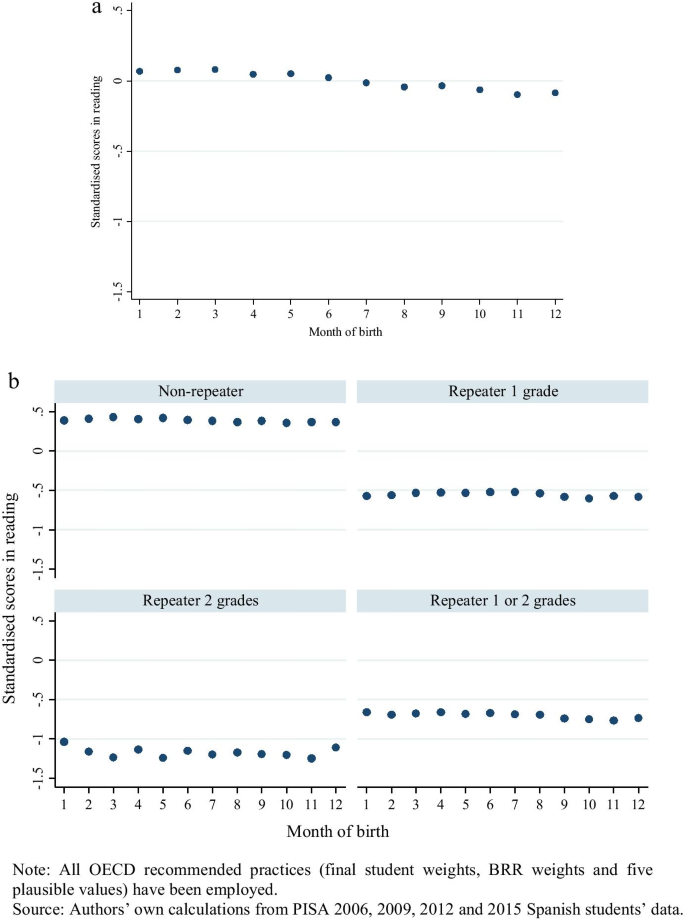
figure2

a Students' standardised scores in reading, complete sample. Note: All OECD recommended practices (final student weights, BRR weights and five plausible values) have been employed. Source: Authors' own calculations from PISA 2006, 2009, 2012 and 2015 Spanish students' data. b Students' standardised scores in reading by grade retention. Note: All OECD recommended practices (final student weights, BRR weights and five plausible values) have been employed. Source: Authors' own calculations from PISA 2006, 2009, 2012 and 2015 Spanish students' data

Full size image

Fig. 3
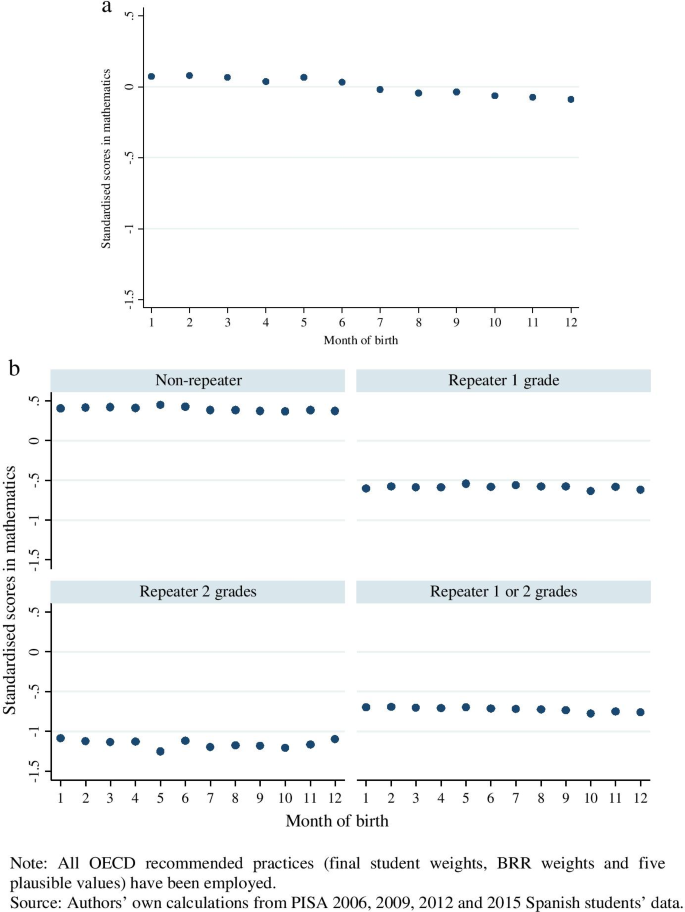
figure3

a Students' standardised scores in mathematics, complete sample. Note: All OECD recommended practices (final student weights, BRR weights and five plausible values) have been employed. Source: Authors' own calculations from PISA 2006, 2009, 2012 and 2015 Spanish students' data. b Students' standardised scores in mathematics by grade retention. Note: All OECD recommended practices (final student weights, BRR weights and five plausible values) have been employed. Source: Authors' own calculations from PISA 2006, 2009, 2012 and 2015 Spanish students' data

Full size image

Fig. 4
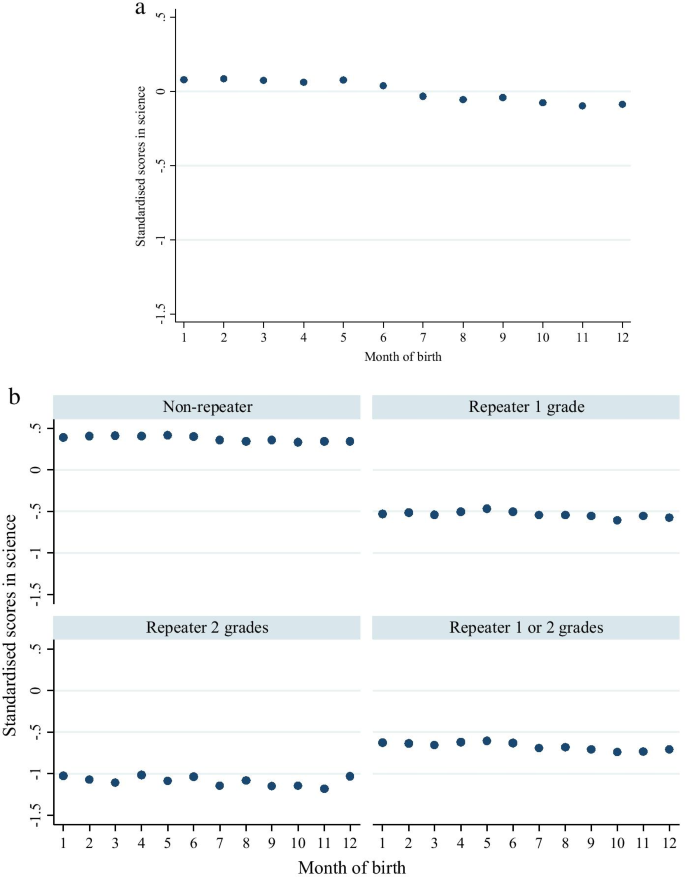
figure4

a Students' standardised scores in science, complete sample. Note: All OECD recommended practices (final student weights, BRR weights and five plausible values) have been employed. Source: Authors' own calculations from PISA 2006, 2009, 2012 and 2015 Spanish students' data. b Students' standardised scores in science by grade retention. Note: All OECD recommended practices (final student weights, BRR weights and five plausible values) have been employed. Source: Authors' own calculations from PISA 2006, 2009, 2012 and 2015 Spanish students' data

Full size image

Table 2 Relationship between students' month of birth and students' competences

Full size table

Therefore, it seems that younger students present lower competences in PISA due to being more likely to repeat a grade, rather than due to their month of birth per se. A possible explanation may be that repeater students are completing a test targeted at tenth grade students, when they are only attending ninth or eighth grade. This may reflect that these students may not have received instruction in certain topics covered by the PISA test. This argument is reinforced by the fact that students repeat in Spain mostly due to a lack of knowledge, and not because of a lack of skills (to the extent that lessons and exams are mostly based on content knowledge rather than in competences; Jerrim et al., 2019; Marcenaro-Gutierrez & Vignoles, 2014). Hence, these students may not have complied with the content knowledge required for their grade.

Robustness checks

We have replicated our estimations using an unconditional regression discontinuity approach (i.e. without any additional controls—the only covariate being students' month of birth). These results are presented in Table 3 and are similar to those presented in Table 1.

Table 3 Relationship between students' month of birth and likelihood of grade retention

Full size table

The next two robustness checks are presented in Table 4. In these, we divide our sample by sex and socio-economic status tertile. Broadly similar results emerge for boys and girls. On the other hand, higher socio-economic status students seem to suffer less harm by being relatively young compared to their school peers in terms of grade retention. Interestingly, it is the middle socio-economic group that has the strongest link between birth month and grade retention.

Table 4 Relationship between students' month of birth and likelihood of grade retention by sex and socio-economic status tertile

Full size table

As a placebo test, we have replicated our estimations using August and September as a cut-off to divide children into groups, rather than December and January. These months have been chosen for our placebo test given that students start 1st grade in September of their sixth birthday. These results are presented in Table 5. As expected, we do not find any significant association with grade retention when using this alternative cut-off. In other words, our placebo test supports our assumption that the December/January birth month captures "exogenous variation".

Table 5 Relationship between students' month of birth and likelihood of grade retention, August–September cut-off

Full size table

Discussion and conclusions

In this paper, we have investigated whether the school entry cut-off set in Spanish law is artificially leading students to repeat a grade. This research is novel in using a methodology which gets closer to capturing a causal effect in the context of Spain. Moreover, by drawing data from four PISA cycles (2006, 2009, 2012 and 2015), we maximise the precision of our results. Our main analysis reveals that Spain's education laws seem to be harming students born late in the year, to the extent that they are more likely to repeat a grade. This is consistent with evidence from other countries (e.g. Bernardi, 2014; Cook & Kang, 2016; Dicks & Lancee, 2018) despite the fact that, in Spain, children's month of birth does not seem to be related to socio-economic status. In particular, younger students are 4.3% more likely to repeat once and 4.8% more likely to repeat twice than older students. These are much more modest estimates than those obtained by Pedraja-Chaparro et al. (2015), who used a simple regression approach and found that younger students were between 70 and 80% more likely to repeat a grade than older students.

Several robustness checks have confirmed our results. We have also found that students of similar age (15 years old) in the same grade (8th, 9th or 10th grade) have similar PISA test scores regardless of their month of birth. This may suggest that younger students achieve lower scores simply due to their increased likelihood of repeating a grade, rather than being due to their age per se (as previously argued by Sprietsma, 2010). Grade retention due to the earlier school enrolment of younger students may therefore be a negative and unfair treatment to these students.

Regarding the school entry cut-off, changing the starting date may seem a potential solution. Yet setting the school entry cut-off at any other date would simply transfer the problem to another point in the school year. Consequently, authors such as Bedard and Dhuey (2012) suggest that delaying school entry for younger students might be beneficial. This would allow younger students to start school some months later, narrowing the differences between the youngest and oldest pupils in a cohort (as shown by Dobkin & Ferreira, 2010, or Robertson, 2011). One implication of this would be that classes would have a higher average age, with similar differences in absolute age between students, but proportionally smaller in terms of development. An argument in favour of this approach is that younger students may tend to perform on par with older students over time, as differences in terms of maturity would shrink when students grow older. Therefore, changing the school entry cut-off within the same year to other does not seem useful, but delaying school entry for younger students might be.

Another option could be implementing a policy which allows parents to delay the enrolment of their children in school, particularly when they are born close to the school entry cut-off (e.g. those born in December). In order to support such an important decision with objective criteria, children may take tests before starting school. Results from such tests could then be used to check whether students are sufficiently prepared to start school. If they are not, then this may be used to support the decision of delaying students' school enrolment. Regardless of the approach used, it is vital that policymakers inform families about this school entry issue and to make school entry laws more flexible. It is particularly important that parents of younger children are able to choose whether to delay their school enrolment or not.

The practice of grade retention has been questioned in previous literature and, as indicated by Andrew (2014), could provoke a scar on students' educational career. If the practice of grade retention is kept in Spain, policymakers might reconsider how it is being conducted. As González-Betancor and López-Puig (2016) highlight, grade retention often means just making students do the same things again the following academic year, instead of trying to develop their skills in a different way. This usual approach may be the easiest solution, as students can be placed in another class in the grade they already attended, without providing any additional materials or resources (Jimerson & Kaufman, 2003). Yet, although repeater students may progress in the repeated year, they have been found to be more likely to have worse outcomes again in subsequent grades (Jimerson & Kaufman, 2003). Education policies that can facilitate the academic progress of these students are hence needed; currently, adults in Spain are failing to provide adequate support to facilitate their development (Jimerson et al., 2005).

More than anything, evidence-based policy reforms to grade retention in Spain are needed, ranging from remedial education (Jimerson, 2001) to the previously described early childhood interventions (García-Pérez et al., 2014; Ou & Reynolds, 2010). Screening and diagnosing the potential learning difficulties of students as early as possible may also help avoid grade retention and its negative influences (González-Betancor & López-Puig, 2016; Mattison et al., 2018). Others have suggested that summer school programmes and academic and behavioural support may also be beneficial (Bowman, 2005; Jimerson & Ferguson, 2007; Mattison et al., 2018).

Of course, a more radical solution would be for Spain to remove grade retention completely, with all students allowed to progress to the next academic year. As indicated by Tingle et al. (2012), if students are not retained, some will then face unique challenges. This includes having to master foundational material while also having to learn more advanced content at the same time. If such a policy was introduced, then it is likely that some students would need special attention and support, including the use of different instructional strategies.

It is important that these policy recommendations are interpreted in light of the limitations of this research. First, we do not have information on students' exact day of birth. Nevertheless, we believe that our use of month of birth is sufficient to provide robust and reliable results. Second, we do not have information on students' pre-school attendance (i.e. in pre-primary education Footnote 19). Such information could have been useful, as previous literature has indicated that attending pre-primary education may help younger students to close their relative disadvantage with older students (Datar, 2006; Fletcher & Kim, 2016; González-Betancor & López-Puig, 2015; Hidalgo-Hidalgo & García-Pérez, 2012; Lubotsky & Kaestner, 2016). Third, we are working with a sample of students and, although we are using four PISA cycles and the OECD assures that PISA has good properties in representing the population, these results should be taken with caution, as there may be some other unobservables which we are not able to control for. Finally, our analysis focuses upon the Spanish education system. Although this work may have better internal validity than previous research, the results may not be readily applicable to other education systems (i.e. they have low external validity).

Despite these limitations, our results show that Spanish school entry laws may be artificially creating grade repeaters from those students unlucky enough to be born at a particular point in the year. This may prevent them forming the same academic abilities had they been born earlier in the year. This, in turn, means that Spain may not be making the most of its human resources, losing potential talent to the detriment of wider society.

Future research could focus upon the implementation of the previously described school entry cut-off and grade retention interventions in Spain using an experimental design. This would allow estimation of their causal effect. The approach used in this study may also be extended to other countries, to investigate whether similar results continue to hold in other school systems and national settings.

Notes

  1. 1.

    This is only true if the student has turned 6 by the end of March.

  2. 2.
  3. 3.

    This stands for "Comisiones Obreras" in Spanish, or Workers' Sindicate.

  4. 4.

    They are required to start that grade approximately in the middle of September of that year.

  5. 5.

    The school entry criterion in France is similar to that in Spain.

  6. 6.

    The school entry criterion in Italy is similar to that in Spain.

  7. 7.

    According to Fiorini and Stevens (2014), Barua and Lang (2016) or Dhuey, Figlio, Karbownik, and Roth (2019), the monotonicity property is fundamental to making regression discontinuity work. This property is defined by Fiorini and Stevens (2014, p. 2) as "for a given change in the value of the instrument, it cannot be that some individuals increase treatment intensity while others decrease treatment intensity" or by Barua and Lang (2016, p. 348) as "while the instrument may have no effect on some individuals, all of those who are affected should be affected unidirectionally".

  8. 8.

    In Spain, compulsory education is divided into primary and secondary education. Primary education has 6 grades (1st to 6th grade) and secondary education has 4 grades (7th to 10th grade).

  9. 9.

    Data for Spain in PISA 2018 is also available; nevertheless, some issues were found with this data for Spain by the OECD (OECD, 2019); hence, we are cautious and stick to the reliable Spanish data of these PISA cycles.

  10. 10.

    In particular, these BRR weights account for the multi-level structure of the data correcting standard errors in a more precise way than using multi-level models (OECD, 2017).

  11. 11.

    BOE stands for "Boletín Oficial del Estado", which is an official daily publication of approved legislations for Spain.

  12. 12.

    BOE (2002, art. 17.3), BOE (2006, art. 20.2) and BOE (2013, art. 20.2).

  13. 13.

    BOE (2002, art. 29.3), BOE (2006, art. 28.5) and BOE (2013, art. 28.5).

  14. 14.

    Students also have to repeat if they fail both reading and mathematics subjects.

  15. 15.

    When students from a single grade are sampled, same-age grade repeaters are lost (as they are attending a lower grade).

  16. 16.

    The OECD created a socio-economic status (ESCS) index with mean 0 and standard deviation 1 using the highest education of parents, the highest parental occupation and home possessions (including the number of books at home, among other resources), by the use of a principal component analysis.

  17. 17.

    Stata has been used to perform all estimations. The syntax and files to reproduce our results are available as Online Supplemental Material. PISA databases to run this syntax are publicly available from the official PISA webpage: https://www.oecd.org/pisa/data/

  18. 18.

    Some previous research has highlighted this reduction in the disadvantage presented by younger students in higher grades. For instance, Robertson (2011), Mühlenweg, Blomeyer, Stichnoth, and Laucht (2012) and Dobkin and Ferreira (2010). The latter did not find any significant influence even on labour market outcomes, such as wages or the probability of employment.

  19. 19.

    This education receives different denominations depending on the country, as, e.g., early childhood education.

References

  1. Agasisti, T., & Cordero-Ferrera, J. M. (2013). Educational disparities across regions: A multilevel analysis for Italy and Spain. Journal of Policy Modeling, 35(6), 1079–1102. https://doi.org/10.1016/j.jpolmod.2013.07.002

    Article  Google Scholar

  2. Alet, E. (2010). Is grade repetition a second chance? Toulouse School of Economics Working Paper, 1–53.

  3. Allen, C. S., Chen, Q., Willson, V. L., & Hughes, J. N. (2009). Quality of research design moderates effects of grade retention on achievement: A meta-analytic, multilevel analysis. Educational Evaluation and Policy Analysis, 31(4), 480–499. https://doi.org/10.3102/0162373709352239

    Article  Google Scholar

  4. Anders, J., Jerrim, J., & McCulloch, A. (2016). How much progress do children in Shanghai make over one academic year? Evidence from PISA. AERA Open, 2(4), 1–13. https://doi.org/10.1177/2332858416678841

    Article  Google Scholar

  5. Andrew, M. (2014). The scarring effects of primary-grade retention? A study of cumulative advantage in the educational career. Social Forces, 93(2), 653–685. https://doi.org/10.1093/sf/sou074

    Article  Google Scholar

  6. Angrist, J. D., & Krueger, A. B. (1991). Does compulsory school attendance affect schooling and earnings? The Quarterly Journal of Economics, 106(4), 979–1014. https://doi.org/10.2307/2937954

    Article  Google Scholar

  7. Asteriou, D., & Agiomirgianakis, G. M. (2001). Human capital and economic growth: Time series evidence from Greece. Journal of Policy Modeling, 23(5), 481–489. https://doi.org/10.1016/S0161-8938(01)00054-0

    Article  Google Scholar

  8. Barua, R., & Lang, K. (2016). School entry, educational attainment and quarter of birth: A cautionary tale of a local average treatment effect. Journal of Human Capital, 10(3), 347–376. https://doi.org/10.1086/687599

    Article  Google Scholar

  9. Bedard, K., & Dhuey, E. (2006). The persistence of early childhood maturity: International evidence of long-run age effects. The Quarterly Journal of Economics, 121(4), 1437–1472. https://doi.org/10.1093/qje/121.4.1437

    Article  Google Scholar

  10. Bedard, K., & Dhuey, E. (2012). School-entry policies and skill accumulation across directly and indirectly affected individuals. Journal of Human Resources, 47(3), 643–683. https://doi.org/10.3368/jhr.47.3.643

    Article  Google Scholar

  11. Bernardi, F. (2014). Compensatory advantage as a mechanism of educational inequality. Sociology of Education, 87(2), 74–88. https://doi.org/10.1177/0038040714524258

    Article  Google Scholar

  12. BOE (2002). Organic Law 10/2002, 23rd December, of the Quality of Education (LOCE). Spain: Nº 307, 24th December 2002, 45188–45220.

  13. BOE (2006). Organic Law 2/2006, 3rd May, of Education (LOE). Spain: Nº 106, 4th May 2006, 17158–17207.

  14. BOE (2013). Organic Law 8/2013, 9th December, for the improvement of the education quality (LOMCE). Nº 295, 10th December 2013, 97858–97921. Spain.

  15. Bowman, L. J. (2005). Grade retention: Is it a help or hindrance to student academic success? Preventing School Failure: Alternative Education for Children and Youth, 49(3), 42–46. https://doi.org/10.3200/psfl.49.3.42-46

    Article  Google Scholar

  16. Buckles, K. S., & Hungerman, D. M. (2013). Season of birth and later outcomes: Old questions, new answers. The Review of Economics and Statistics, 95(3), 711–724. https://doi.org/10.1162/REST_a_00314

    Article  Google Scholar

  17. Cabus, S. J., & De Witte, K. (2012). Naming and shaming in a 'fair' way. On disentangling the influence of policy in observed outcomes. Journal of Policy Modeling, 34(5), 767–787. https://doi.org/10.1016/j.jpolmod.2012.03.001

    Article  Google Scholar

  18. Calero, J., Choi, A., & Waisgrais, S. (2010). Determinants of the school failure risk in Spain: A multilevel logistic model approach to PISA-2006. Revista de Educación, Extraordinary vol., 225–256.

  19. Carabaña, J. (2013). Repetición de curso y puntuaciones pisa ¿cuál causa cuál? In INEE (Eds.), PISA 2012: Programa para la evaluación internacional de los alumnos. Informe español. Volumen II: Análisis secundario (pp. 32–66). Madrid: Ministerio de Educación, Cultura y Deporte, Instituto Nacional de Evaluación Educativa.

  20. CCOO. (2018). Fracaso Escolar y Abandono Educativo Temprano. Federación de Enseñanza de CCOO.

    Google Scholar

  21. Choi, A., Gil, M., Mediavilla, M., & Valbuena, J. (2016). Double toil and trouble: Grade retention and academic performance. Document de treball de l'IEB 2016/17, 1–28

  22. Cook, P. J., & Kang, S. (2016). Birthdays, schooling, and crime: Regression-discontinuity analysis of school performance, delinquency, dropout, and crime initiation. American Economic Journal: Applied Economics, 8(1), 33–57. https://doi.org/10.1257/app.20140323

    Article  Google Scholar

  23. Crawford, C., Dearden, L., & Greaves, E. (2014). The drivers of month-of-birth differences in children's cognitive and non-cognitive skills. Journal of the Royal Statistical Society: Series A (statistics in Society), 177(4), 829–860. https://doi.org/10.1111/rssa.12071

    Article  Google Scholar

  24. Datar, A. (2006). Does delaying kindergarten entrance give children a head start? Economics of Education Review, 25(1), 43–62. https://doi.org/10.1016/j.econedurev.2004.10.004

    Article  Google Scholar

  25. Dhuey, E., Figlio, D., Karbownik, K., & Roth, J. (2019). School starting age and cognitive development. Journal of Policy Analysis and Management, 38(9), 538–578. https://doi.org/10.1002/pam.22135

    Article  Google Scholar

  26. Diaz, J., Grau, N., Reyes, T., & Rivera, J. (2016). The impact of grade retention on juvenile crime (pp. 1–58). University of Chile, Department of Economics Working Papers wp429.

    Google Scholar

  27. Dicks, A., & Lancee, B. (2018). Double disadvantage in school? Children of immigrants and the relative age effect: A regression discontinuity design based on the month of birth. European Sociological Review, 34(3), 319–333. https://doi.org/10.1093/esr/jcy014

    Article  Google Scholar

  28. DiPrete, T. A., & Eirich, G. M. (2006). Cumulative disadvantage as a mechanism for inequality: A review of theoretical and empirical developments. Annual Review of Sociology, 32, 271–297. https://doi.org/10.1146/annurev.soc.32.061604.123127

    Article  Google Scholar

  29. Dobkin, C., & Ferreira, F. (2010). Do school entry laws affect educational attainment and labor market outcomes? Economics of Education Review, 29(1), 40–54. https://doi.org/10.1016/j.econedurev.2009.04.003

    Article  Google Scholar

  30. Eide, E. R., & Showalter, M. H. (2001). The effect of grade retention on educational and labor market outcomes. Economics of Education Review, 20(6), 563–576. https://doi.org/10.1016/S0272-7757(00)00041-8

    Article  Google Scholar

  31. Eren, O., Depew, B., & Barnes, S. (2017). Test-based promotion policies, dropping out, and juvenile crime. Journal of Public Economics, 153, 9–31. https://doi.org/10.1016/j.jpubeco.2017.07.002

    Article  Google Scholar

  32. Eurydice. (2011). Grade retention during compulsory education in Europe: Regulations and statistics. Brussels: Education, Audiovisual and Culture Executive Agency. https://doi.org/10.2797/50570

    Book  Google Scholar

  33. Fiorini, M., & Stevens, K. (2014). Assessing the monoticity assumption in IV and fuzzy RD designs. The University of Sydney Economics Working Paper Series, 13, 1–52.

  34. Fletcher, J., & Kim, T. (2016). The effects of changes in kindergarten entry age policies on educational achievement. Economics of Education Review, 50, 45–62. https://doi.org/10.1016/j.econedurev.2015.11.004

    Article  Google Scholar

  35. García-Pérez, J. I., Hidalgo-Hidalgo, M., & Robles-Zurita, J. A. (2014). Does grade retention affect achievement? Some Evidence from Spain. Applied Economics, 46(12), 1373–1392. https://doi.org/10.1080/00036846.2013.872761

    Article  Google Scholar

  36. Glick, P., & Sahn, D. E. (2010). Early academic performance, grade repetition, and school attainment in Senegal: A panel data analysis. The World Bank Economic Review, 24(1), 93–120. https://doi.org/10.2307/40647422

    Article  Google Scholar

  37. González-Betancor, S. M., & López-Puig, A. J. (2015). Escolarización temprana, trimestre de nacimiento y rendimiento educativo en primaria. Revista De Educación, 369, 159–183. https://doi.org/10.4438/1988-592X-RE-2015-369-294

    Article  Google Scholar

  38. González-Betancor, S. M., & López-Puig, A. J. (2016). Grade retention in primary education is associated with quarter of birth and socioeconomic status. PLoS One, 11(11), e0166431. https://doi.org/10.1371/journal.pone.0166431

    Article  Google Scholar

  39. Goos, M., Schreier, B. M., Knipprath, H. M. E., De Fraine, B., Van Damme, J., & Trautwein, U. (2013). How can cross-country differences in the practice of grade retention be explained? A closer look at national educational policy factors. Comparative Education Review, 57(1), 54–84. https://doi.org/10.1086/667655

    Article  Google Scholar

  40. Gortazar, L. (2019). ¿Favorece el sistema educativo español la igualdad de oportunidades? FEDEA, Estudios sobre la Economía Española no. 2019/17, Madrid.

  41. Hidalgo‐Hidalgo, M., & García‐Pérez, J. I. (2012). Impacto de la asistencia a educación infantil sobre los resultados académicos del estudiante en primaria. In MECD (Ed.), PIRLS - TIMSS 2011. Volumen II: Informe Español. Análisis Secundario (pp. 83–113). Madrid: Instituto Nacional de Evaluación Educativa.

  42. IECA (2021). Premature dropout rate by sex. Last accessed July 2021 from http://www.juntadeandalucia.es/institutodeestadisticaycartografia/indsoc/indicadores/1038.htm

  43. Jacob, B. A., & Lefgren, L. (2009). The effect of grade retention on high school completion. American Economic Journal: Applied Economics, 1(3), 33–58. https://doi.org/10.1257/app.1.3.33

    Article  Google Scholar

  44. Jerrim, J., Lopez-Agudo, L. A., & Marcenaro-Gutiérrez, O. D. (2019). The relationship between homework and the academic progress of children in Spain during compulsory elementary education: A twin fixed-effects approach. British Educational Research Journal, 45(5), 1021–1049. https://doi.org/10.1002/berj.3549

    Article  Google Scholar

  45. Jerrim, J., Lopez-Agudo, L. A., Marcenaro-Gutierrez, O. D., & Shure, N. (2017). What happens when econometrics and psychometrics collide? An example using the PISA data. Economics of Education Review, 61, 51–58. https://doi.org/10.1016/j.econedurev.2017.09.007

    Article  Google Scholar

  46. Jimerson, S. R. (2001). Meta-analysis of grade retention research: Implications for practice in the 21st century. School Psychology Review, 30(3), 420–437.

    Article  Google Scholar

  47. Jimerson, S. R., & Ferguson, P. (2007). A longitudinal study of grade retention: Academic and behavioral outcomes of retained students through adolescence. School Psychology Quarterly, 22(3), 314–339. https://doi.org/10.1037/1045-3830.22.3.314

    Article  Google Scholar

  48. Jimerson, S. R., & Kaufman, A. M. (2003). Reading, writing, and retention: A primer on grade retention research. The Reading Teacher, 56(7), 622–635.

    Google Scholar

  49. Jimerson, S. R., Pletcher, S. M. W., Graydon, K., Schnurr, B. L., Nickerson, A. B., & Kundert, D. K. (2005). Beyond grade retention and social promotion: Promoting the social and academic competence of students. Psychology in the Schools, 43(1), 85–97. https://doi.org/10.1002/pits.20132

    Article  Google Scholar

  50. Klapproth, F., & Schaltz, P. (2015). Who is retained in school, and when? Survival analysis of predictors of grade retention in Luxembourgish secondary school. European Journal of Psychology of Education, 30, 119–136. https://doi.org/10.1007/s10212-014-0232-7

    Article  Google Scholar

  51. Lubotsky, D., & Kaestner, R. (2016). Do 'Skills Beget Skills'? Evidence on the effect of kindergarten entrance age on the evolution of cognitive and non-cognitive skill gaps in childhood. Economics of Education Review, 53, 194–206. https://doi.org/10.1016/j.econedurev.2016.04.001

    Article  Google Scholar

  52. Manacorda, M. (2012). The cost of grade retention. Review of Economics and Statistics, 94(2), 596–606. https://doi.org/10.1162/rest_a_00165

    Article  Google Scholar

  53. Marcenaro-Gutierrez, O., & Vignoles, A. (2014). A comparison of teacher and test-based assessment for Spanish primary and secondary students. Educational Research, 57(1), 1–21. https://doi.org/10.1080/00131881.2014.983720

    Article  Google Scholar

  54. Mariano, L. T., Martorell, P., & Tsai, T. (2018). The effects of grade retention on high school outcomes: Evidence from New York City Schools. RAND Education, WR-1259-DEIES, 1–48.

  55. Martorell, P., & Mariano, L. T. (2018). The causal effects of grade retention on behavioral outcomes. Journal of Research on Educational Effectiveness, 11(2), 192–216. https://doi.org/10.1080/19345747.2017.1390024

    Article  Google Scholar

  56. Mattison, A., Raffaele, L. M., Dedrick, R., Dickinson, S., Wingate, E., & Hanks, C. (2018). Early elementary teacher ratings of behavior as predictors of grade retention: Race, gender, and socioeconomic status as potential moderators. Psychology in the Schools, 55(10), 1171–1187. https://doi.org/10.1002/pits.22192

    Article  Google Scholar

  57. Mühlenweg, A., Blomeyer, D., Stichnoth, H., & Laucht, M. (2012). Effects of age at school entry (ASE) on the development of non-cognitive skills: Evidence from psychometric data. Economics of Education Review, 31(3), 68–76. https://doi.org/10.1016/j.econedurev.2012.02.004

    Article  Google Scholar

  58. OECD (2007). PISA 2006. Volume 2: Data. Paris: OECD Publishing.

  59. OECD. (2009). PISA Data Analysis Manual SPSS® (2nd ed.). OECD Publishing.

    Google Scholar

  60. OECD. (2010). PISA 2009 results: What students know and can do – Student performance in reading, mathematics and science (Volume I). OECD Publishing. https://doi.org/10.1787/9789264091450-en

    Book  Google Scholar

  61. OECD. (2014). PISA 2012 results: What students know and can do – Student performance in mathematics, reading and science (Volume I, Revised edition, February 2014). OECD Publishing. https://doi.org/10.1787/9789264201118-en

    Book  Google Scholar

  62. OECD. (2016). PISA 2015 results (Volume I): Excellence and equity in education. OECD Publishing. https://doi.org/10.1787/9789264266490-en

    Book  Google Scholar

  63. OECD. (2017). PISA 2015 technical report. OECD Publishing.

    Google Scholar

  64. OECD (2019). PISA 2018 in Spain. Paris: OECD Publishing. Retrieved from http://www.oecd.org/pisa/data/PISA2018Spain_final.pdf

  65. Ou, S.-R., & Reynolds, A. J. (2010). Grade retention, postsecondary education, and public aid receipt. Educational Evaluation and Policy Analysis, 32(1), 118–139. https://doi.org/10.3102/0162373709354334

    Article  Google Scholar

  66. Özek, U. (2015). Hold back to move forward? Early grade retention and student misbehavior. Education Finance and Policy, 10(3), 350–377. https://doi.org/10.1162/edfp_a_00166

    Article  Google Scholar

  67. Pedraja-Chaparro, F., Santín, D., & Simancas, R. (2015). Determinants of grade retention in France and Spain: Does birth month matter? Journal of Policy Modeling, 37(5), 820–834. https://doi.org/10.1016/j.jpolmod.2015.04.004

    Article  Google Scholar

  68. Robertson, E. (2011). The effects of quarter of birth on academic outcomes at the elementary school level. Economics of Education Review, 30(2), 300–311. https://doi.org/10.1016/j.econedurev.2010.10.005

    Article  Google Scholar

  69. Schwerdt, G., West, M. R., & Winters, M. A. (2017). The effects of test-based retention on student outcomes over time: Regression discontinuity evidence from Florida. Journal of Public Economics, 152, 154–169. https://doi.org/10.1016/j.jpubeco.2017.06.004

    Article  Google Scholar

  70. Sprietsma, M. (2010). Effect of relative age in the first grade of primary school on long-term scholastic results: International comparative evidence using PISA 2003. Education Economics, 18(1), 1–32. https://doi.org/10.1080/09645290802201961

  71. Tingle, L. R., Schoeneberger, J., & Algozzine, B. (2012). Does grade retention make a difference? The Clearing House: A Journal of Educational Strategies, Issues and Ideas, 85(5), 179–185. https://doi.org/10.1080/00098655.2012.679325

    Article  Google Scholar

  72. Wallingford, E. L., & Prout, H. T. (2000). The relationship of season of birth and special education referral. Psychology in the Schools, 37(4), 379–387. https://doi.org/10.1002/1520-6807(200007)37:4%3c389::aid-pits9%3e3.0.co;2-k

Download references

Funding

This work has been partly supported by FEDER funding (under Research Project PY20-00228), Ministerio de Ciencia e Innovación (under Research Project PID2020-119471RB-I00) and the Andalusian Regional Government (SEJ-645).

Author information

Affiliations

  1. Department of Social Science, UCL Institute of Education, University College London, 20 Bedford Way, London, WC1H 0AL, UK

    John Jerrim

  2. Departamento de Economía Aplicada (Estadística Y Econometría), Facultad de Ciencias Económicas Y Empresariales, Universidad de Málaga, Plaza de El Ejido s/n, 29013, Málaga, España

    Luis Alejandro Lopez-Agudo & Oscar David Marcenaro-Gutierrez

Corresponding author

Correspondence to John Jerrim.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Table

Table 6 Mean differences between those students born in January and December, for Spanish students in PISA 2006, 2009, 2012 and 2015

Full size table

6

Table

Table 7 Descriptive statistics for Spanish students in PISA 2006, 2009, 2012 and 2015

Full size table

7

About this article

Verify currency and authenticity via CrossMark

Cite this article

Jerrim, J., Lopez-Agudo, L.A. & Marcenaro-Gutierrez, O.D. Grade retention and school entry age in Spain: a structural problem. Educ Asse Eval Acc (2021). https://doi.org/10.1007/s11092-021-09375-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI : https://doi.org/10.1007/s11092-021-09375-7

Keywords

  • Grade retention
  • Birth date
  • Regression discontinuity
  • Relative age effect

JEL codes

  • I20
  • I21
  • I28

The Wages of Failure: New Evidence on School Retention and Long-run Outcomes

Source: https://link.springer.com/article/10.1007/s11092-021-09375-7

0 Response to "The Wages of Failure: New Evidence on School Retention and Long-run Outcomes"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel